Zahlenmengen

Zahlenmengen

Menge der natürlichen Zahlen

N = {1, 2, 3, 4, 5, ... }

Die natürlichen Zahlen benutzen wir im Alltag, um Gegenstände zu zählen.

Es gibt unendlich viele natürliche Zahlen. (Manchmal wird die 0 auch dazugerechnet.)

Veranschaulichung auf dem Zahlenstrahl:

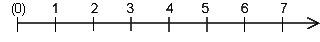
Man kann die natürlichen Zahlen auf verschiedene Art einteilen, z.B.
gerade Zahlen (N_g) und ungerade Zahlen (N_u)
Primzahlen (P) und zusammengesetzte Zahlen
(Jede natürliche Zahl kann eindeutig als Produkt von Primzahlen geschrieben werden, z.B. 60 = 2·2·3·5)

Wenn wir zwei natürliche Zahlen addieren oder multiplizieren, ist das Ergebnis wieder eine natürliche Zahl. Subtraktion ist nicht immer möglich (z.B. 7 - 10 = ?). Daher erweitern wir die natürlichen Zahlen zur

Menge der ganzen Zahlen

Z = { ... -3, -2, -1, 0, 1, 2, 3, ... }

Veranschaulichung auf der Zahlengeraden:

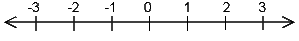
Ganze Zahlen kann man addieren, subtrahieren, man kann sie multiplizieren: Immer wieder entstehen ganze Zahlen. Addition und Multiplikation haben viele Eigenschaften, an die man sich im Lauf der Schulzeit gewöhnt: Es gelten Kommutativ-, Assoziativ- und Distributivgesetz.

Quotienten ganzer Zahlen müssen nicht ganzzahlig sein!

Natürliche Zahlen sind spezielle Beispiele für ganze Zahlen.